Хиросима - Кашима АнтлерсHotline
Hotline
Ноттингем Форест - Манчестер Юн.
Копенгаген - Рандерс
Байер - Бохум
.png)
Аргентина - Brazil
.png)
Македония - Уэльс
Команда
Рефери
Конструктор Матчей
Выберите турнир
Основные
Англия Испания Германия Италия Франция Украина Россия ЯпонияМеждународные (клубы)
Мир Европа Южная Америка Азия Северная Америка Африка ОкеанияСборные
Мир (Сборные) Европа (сборные) Южная Америка (Сборные) Азия (Сборные) С/Ц Америка (Сборные) Африка (Сборные) Океания (Сборные)Европа
Австрия Азербайджан Беларусь Бельгия Босния и Герцеговина Болгария Хорватия Кипр Чехия Дания Эстония Финляндия Грузия Греция Венгрия Исландия Ирландия Израиль Казахстан Латвия Литва Голландия Северная Ирландия Норвегия Польша Португалия Румыния Шотландия Сербия Словакия Словения Швеция Швейцария Турция УэльсЮжная Америка
Аргентина Боливия Бразилия Чили Колумбия Эквадор Парагвай Перу Уругвай ВенесуэлаАзия
Австралия Бахрейн Китай Тайвань Гонконг Индия Индонезия Южная Корея Катар Судовская Аравия Сингапур Таджикистан Таиланд Туркменистан ОАЭСеверная Америка
Канада Коста-Рика El-salvador Гондурас Мексика Никарагуа СШААфрика
Алжир Египет Марокко Нигерия ЮАРОкеания
Новая ЗеландияАналитика
Сравнивать статистику всех команд турнира бывает неудобно, поэтому можно воспольвозоваться фильтром по стадиям турнира. С помощ..
Дата публикации:
23/03/2025
ТОП МАТЧИ
| 19:30 |
|
Атлетико Мад VS Барселона Free! |
45'
| 11:00 |
|
FC Gagra VS Dinamo Tbili |
Инструмент расчета коэффициентов корреляции показателей команды внедрен на странице турнира
16/12/2019
Коэффициент корреляции - показатель, характеризующий силу статистической связи двумя или несколькими случайными величинами.
Значения коэффициента корреляции всегда расположены в диапазоне от -1 до 1 и интерпретируются следующим образом:
- если коэффициент корреляции близок к 1, то между переменными наблюдается положительная корреляция. Иными словами, отмечается высокая степень связи между переменными. В данном случае, если значения переменной x будут возрастать, то и выходная переменная также будет увеличиваться;
- если коэффициент корреляции близок к -1, это означает, что между переменными имеет место сильная отрицательная корреляция. Иными словами, поведение выходной переменной будет противоположным поведению входной. Если значение x будет возрастать, то y будет уменьшаться, и наоборот;
- промежуточные значения, близкие к 0, будут указывать на слабую корреляцию между переменными и, соответственно, низкую зависимость. Иными словами, поведение переменной x не будет совсем (или почти совсем) влиять на поведение y (и наоборот).
Очевидно, что если корреляция между переменными высокая, то, зная поведение входной переменной, проще предсказать поведение выходной, и полученное предсказание будет точнее (говорят, что входная переменная хорошо «объясняет» выходную). Чем выше корреляция наблюдается между переменными, тем очевиднее связь между ними, например, взаимозависимость между ростом и весом людей.
Согласно распространенным оценкам, коэффициент корреляции считается высоким (значимым), если он больше 0.7 (по модулю).
Рассмотрим несколько примеров, как можно использовать корреляцию в анализе футбольной статистики.
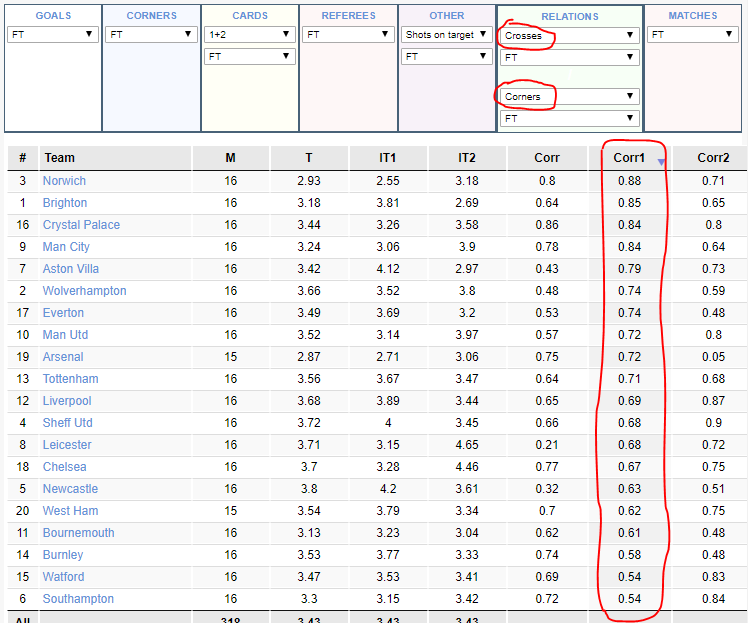
1. На примере английской Премьер лиги проанализируем связь между подачами в штрафную и угловыми. Логично предположить, что между данными показателями должна быть прямая связь (положительная корреляция), ведь чем больше команда сделает подач, тем большая вероятность, что мяч выйдет на угловой. Чтобы увидеть коэффициенты корреляции команд, откроем вкладку Отношения и выберем нужные показатели (корреляция находится в 3 последних столбцах):
Действительно, как видно из скриншота, все команды имеют положительный коэффициент корреляции между подачами и угловыми, но если у Норвича данный коэффициент равняется 0.88, то у Саутгэмптона он только 0.54. То есть, если мы предполагаем, что Норвич в предстоящем матче будет иметь много подач в штрафную (например из-за присутствия в складе сильных фланговых игроков или высоких форвардов), то количество угловых команды тоже должно быть большим.
